The Ulam spiral in Rust
I'd like to share some thoughts about a specific mathematical phenomenon related to the prime numbers and tiny piece of software to generate visual representation of it.
What is specific about prime numbers?
Prime numbers are special subset of natural numbers. A prime number (or a prime as we'll call them) can be divided by 1 or by itself only, leaving no remainder. This simple definition is what most people learn on math lessons and is enough to start thinking about interesting properties of prime numbers.2 3 5 7 11 13 17 19 ...
You can generate infinite number of primes, but...
- Are primes truly random?
- Do they follow any visible pattern?
The spiral and Stanisław Ulam
Person who asked himself those questions was Stanisław Ulam, Polish-American mathematician involved in Project Manhattan. According to the anecdote, he played with numbers during one long and boring lecture in 1963 and tried to arrange prime numbers in spiral-like shape. The result was something like this: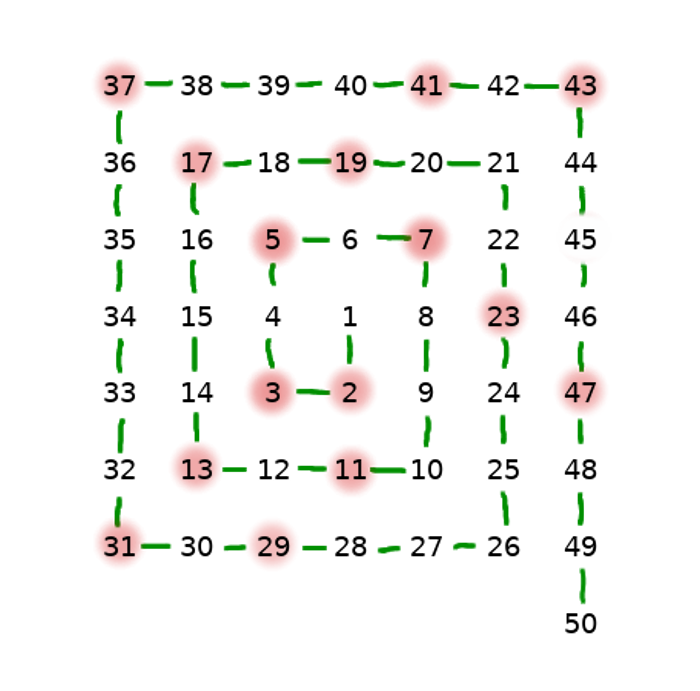
Ulam drew a bigger spiral and noticed that you can notice some interesting features on the picture. Later he together Myron Stein and Mark Wells used the MANIAC II computer (which was state of art computing machine at this time) at Los Alamos Scientific Laboratory to generate spiral with 65 000 points.
When you generate more and more of those numbers, you can see that without any doubt there is a pattern.

First thing that notice is the presence of diagonal lines. What you would expect to see is a random noise, like that below. (I choose only odd numbers to compare because the density is fairly comparable on the image and more importantly all of prime numbers are also odd, except for number 2.)

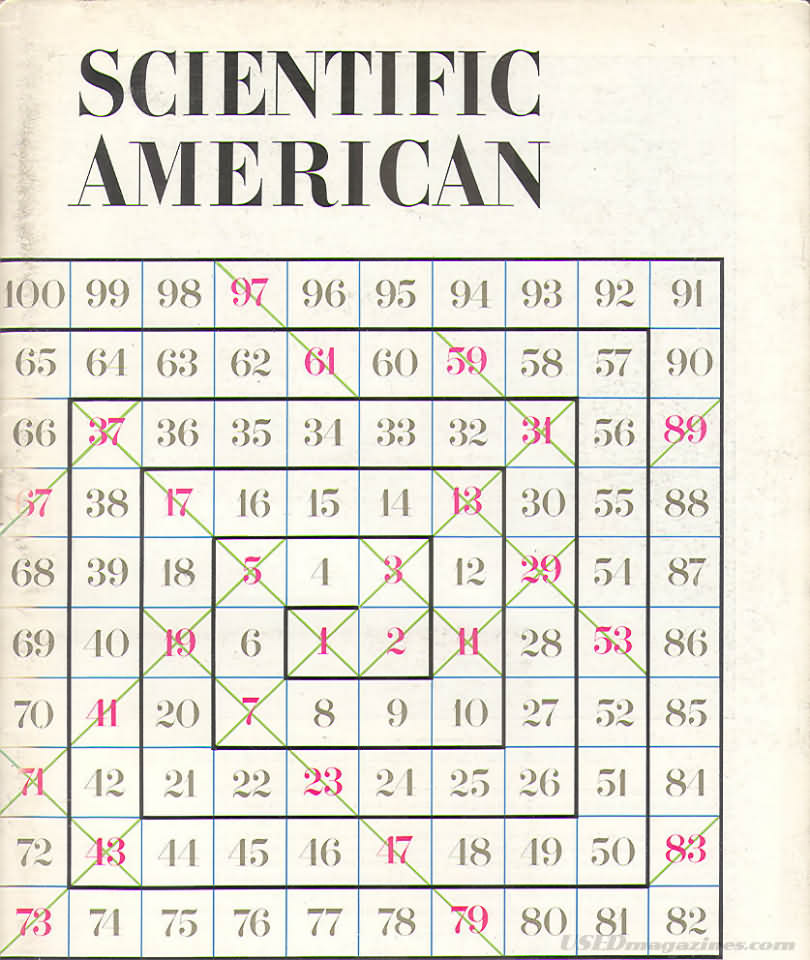
Later the Ulam's idea was popularized by Martin Gardner, very prominent writer from Scientific American (Scientific American 210, 120 - 128 (1964)) and people started to wonder what is causing the prime numbers to form those distinct patterns when drawn into spiral.
Here is the original cover from the Scientific American:
 (source: OEIS)
(source: OEIS)
I will not cover the explanation for the prime spiral mystery, but I can mention that approximate solution is related to the fact that some quadratic polynomials generate great number of primes. You can notice that diagonal lines on the spiral are formed by series of either only odd or even numbers. To learn more, please refer to the Everipedia: Explanation of the Ulam Spiral
Let's see by ourselves
There's always a benefit in skeptical thinking, so why not try to see our own spiral. To generate my own, I used a pretty simple implementation, focused more on readability, rather than performance. I used Rust lang for the algorithm image creation and Gtk layout of the program.How to generate primes?
Sieve of Eratosthenes was the first choice for me.In the modern times we would express the Sieve as a Rust code, like here: 1 pub fn generate_primes(max: u64) -> Vec<u64> {
2 let mut candidates: Vec<u64> = vec![1; max as usize + 1];
3 candidates[0] = 0;
4 candidates[1] = 0;
5 let max_sqrt = (max as f64).sqrt() as u64 + 1;
6
7 for number in 2..max_sqrt {
8 let mut multiplied = number * number;
9 while multiplied < max + 1 {
10 candidates[multiplied as usize] = 0;
11 multiplied += number;
12 }
13 }
14 candidates
15 }
The only optimization I used here is to limit the iteration to the square root of the max, which saves a lot of computations.
The output of the function would look like this:1 vec![0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
Algorithm for generating the spiral
It was inspired by the observation that a spiral is a kind of imperfect square which has always one side longer, like on the picture. When the side gets longer? Exactly after two turns.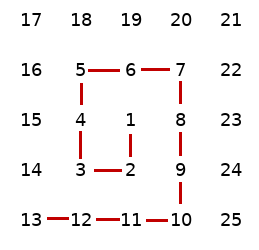
Here's what we do:
- For all directions (down, left, up, right) walk exactly this many times as is the current side length of the spiral.
- Every second turn add one step to the length, so that we don't overlap the existing spiral.
- Every time you make a step, pick a element from the array (Vec in our case) and check if the number is a prime. If yes, then paint a pixel.
1 let directions = &["down", "left", "up", "right"];
2
3 while !stop {
4
5 for direction in directions {
6 turn += 1;
7 for _ in 0..times {
8 if counter < numbers_len {
9 stop = self.move_cursor(&mut x, &mut y, direction);
10 if numbers[counter] == 1 {
11 img.put_pixel(x, y, pixel)
12 }
13 counter += 1;
14 }
15 }
16 if turn == 2 {
17 times += 1;
18 turn = 0;
19 }
20 }
21 if (counter >= numbers_len) | (x <= 2) {
22 stop = true;
23 }
24 }
The output of the function that generates the primes is an ImageBuffer containing the Vec with RGB information about all pixels.
1 image::ImageBuffer<image::Rgb<u8>, Vec<u8>>
Later the buffer can be used for two purposes:
- Save the data as the png file
- Show the image in the window
Here's the result!
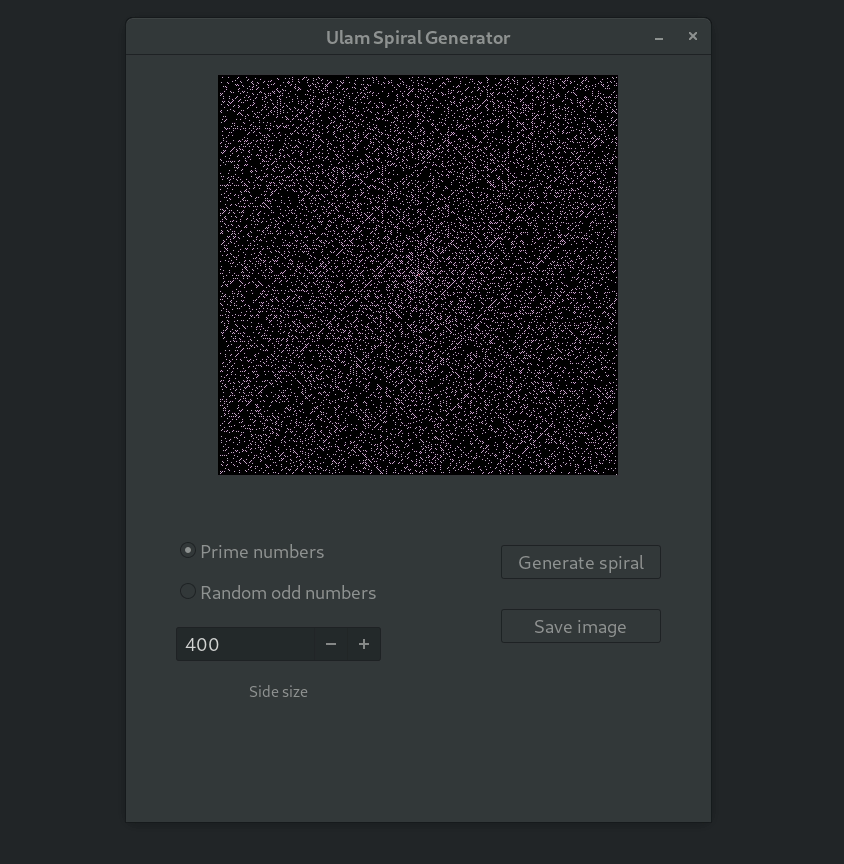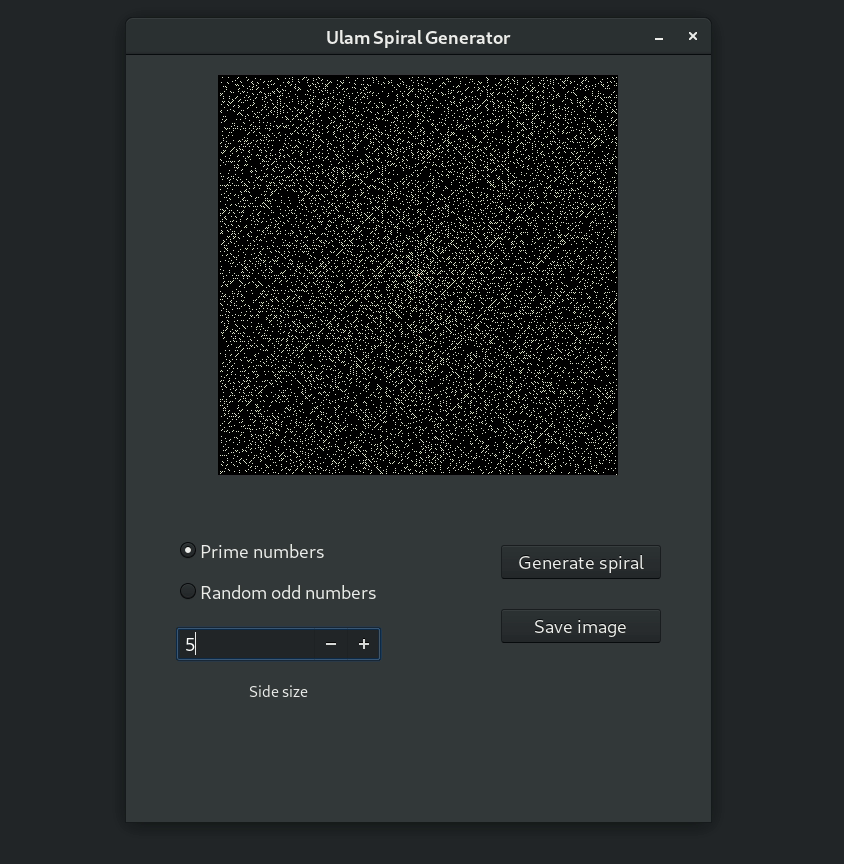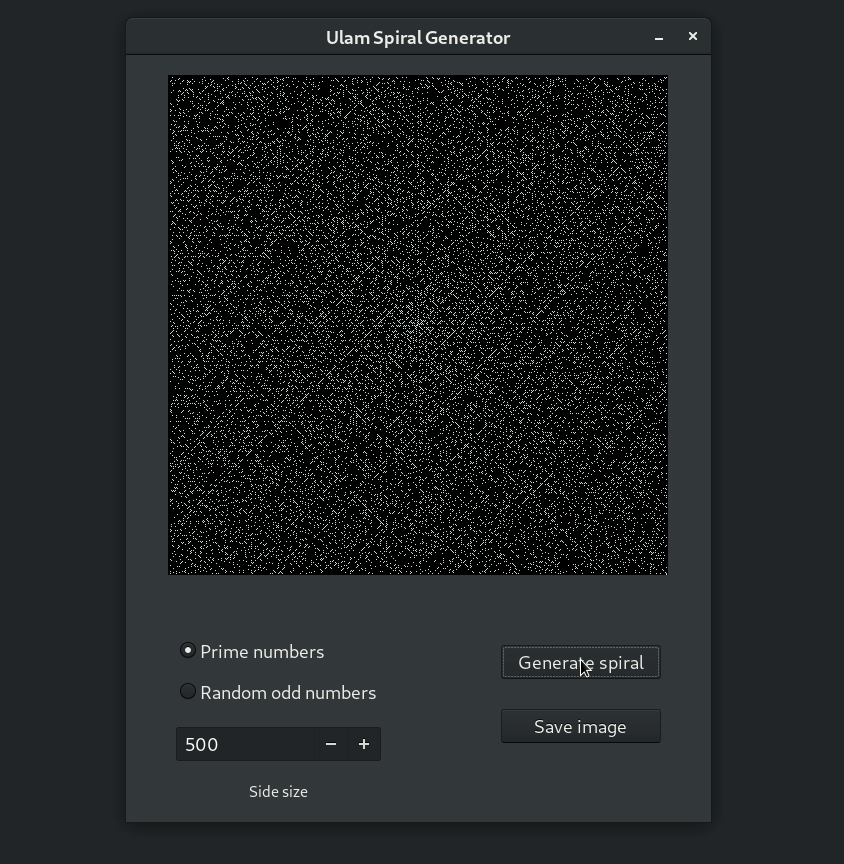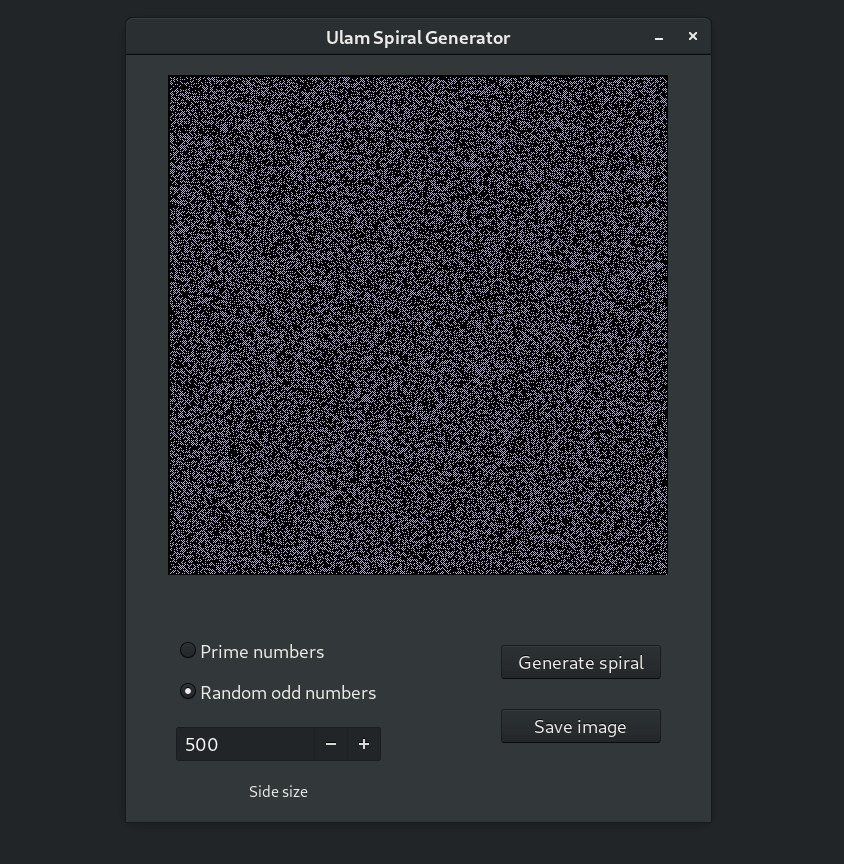
What did not work as expected
I tried to write functionality of generating the rectangular spiral with different aspect ratios. It sounded easy (just divide width by height and use the ratio to get the length of horizontal or vertical side). In fact it was way more difficult and I had trouble debugging why the pattern looked like this:
After having some hard time with the code I decided that this feature is not so cool to spend more time on it. Don't try to fix something that is GOOD ENOUGH.
In my opinion it's really important to show not only successful results in software engineering, but also the failures. They are also part of the job and they tell the story about the amount of time and effort that was spent overall on some task.
In the next post I'll give some more details about the Rust programming with Gtk, which was pretty exciting, but also a bit challenging.
Source code
https://github.com/sireliah/ulam-spiralSources:
Ulam Spiral on WikipediaUlam Spiral on Everipedia
The On-Line Encyclopedia of Integer Sequences
Nicomachus of Gerasa the Neo Pythagorean Introduction to Arithmetic
